Documentation Powered by ReDoc

星尘数据 - 数据结构文档 (v1.0)

Download OpenAPI specification:Download

欢迎来到星尘数据，这里是我们的导入导出数据结构文档

[中文版本] [English Version]

点云类

点云导入数据结构

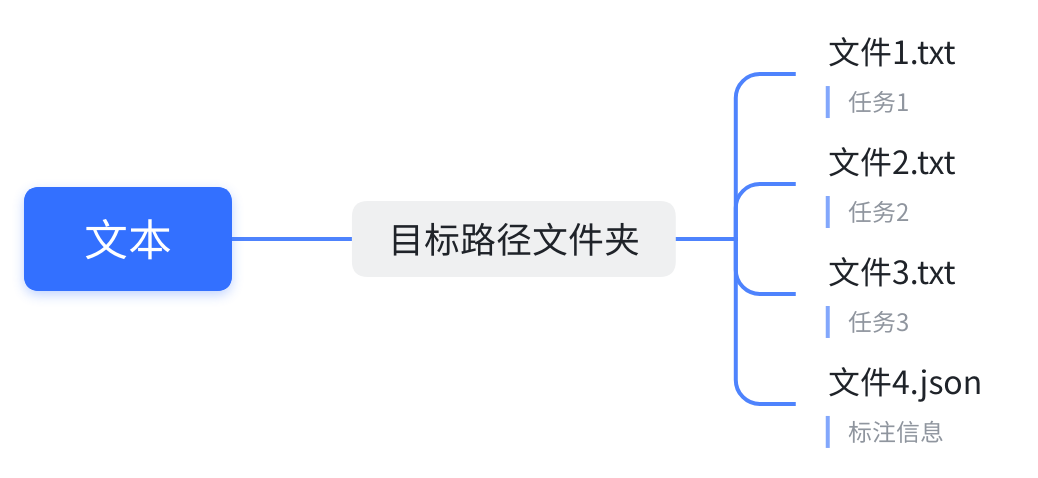
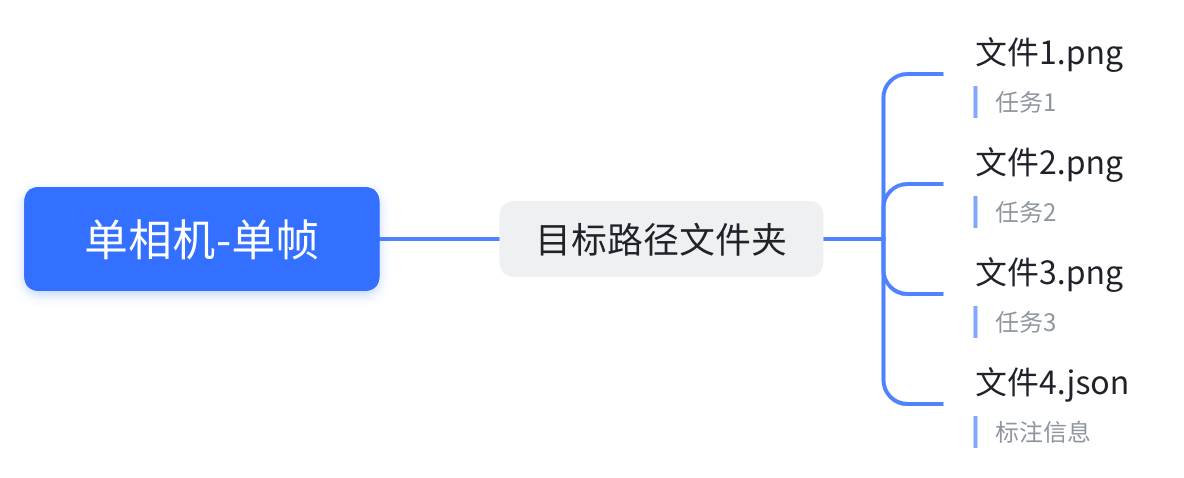
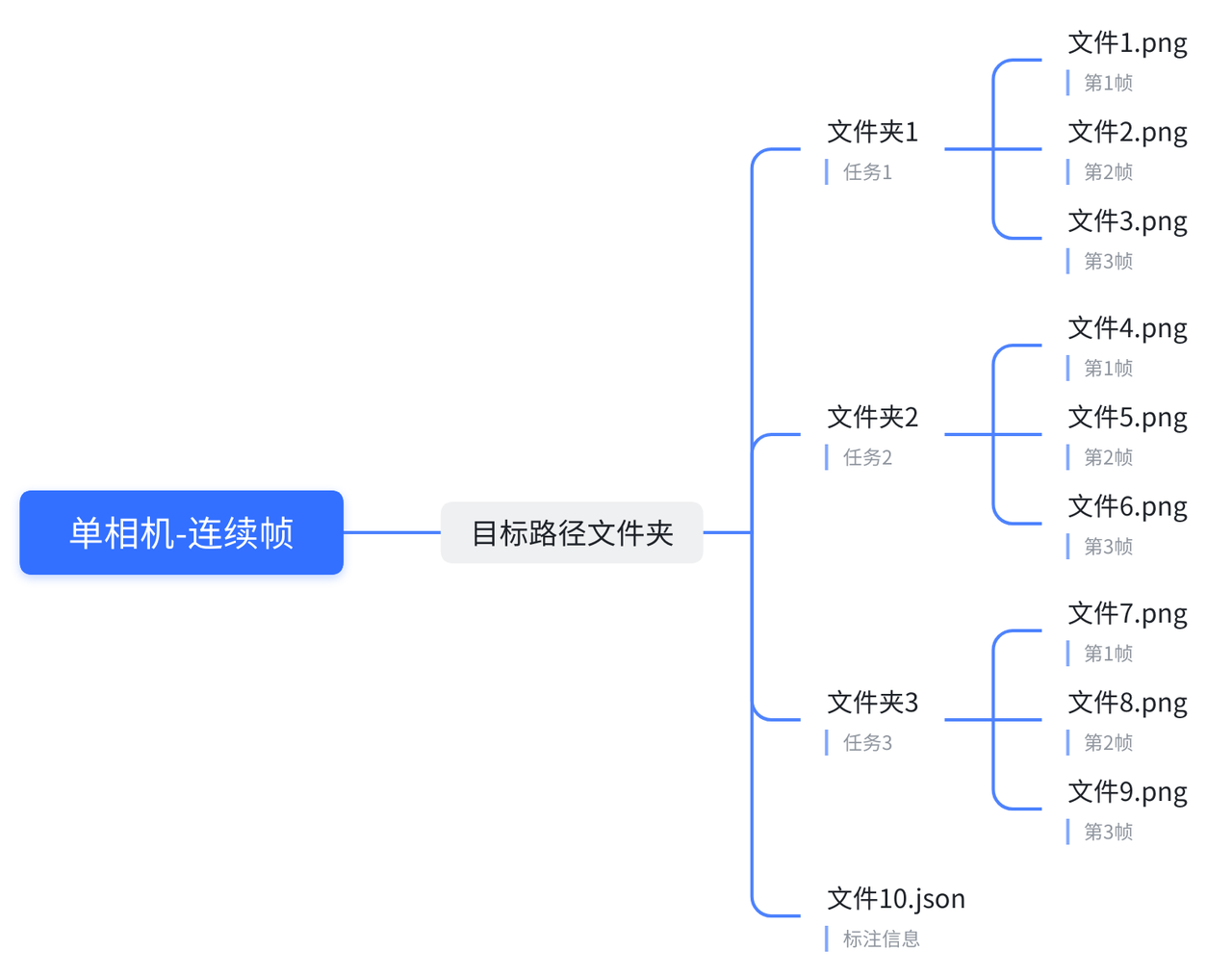
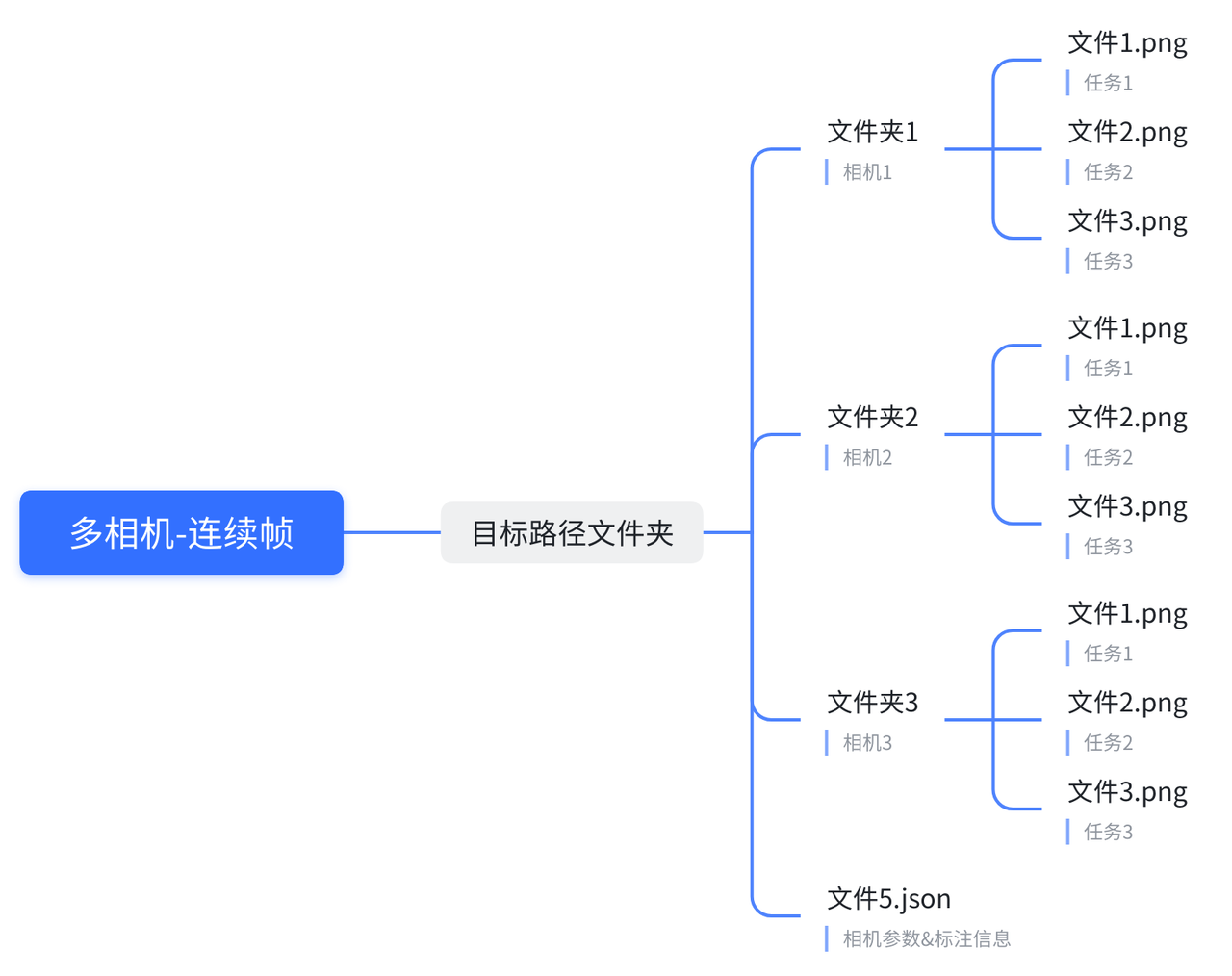
请以以下格式给到数据，这将方便我们以最快的速度进行数据适配

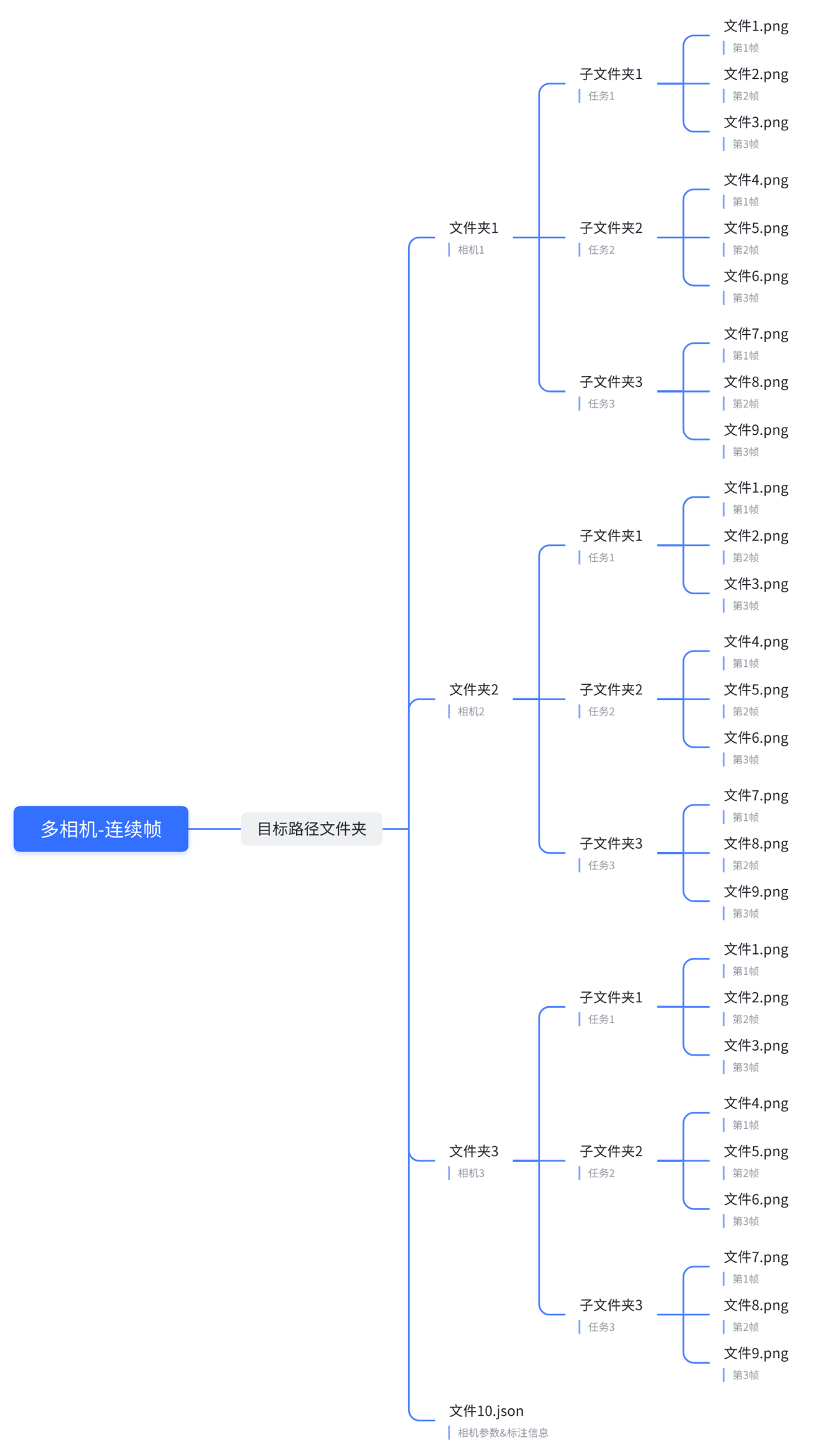
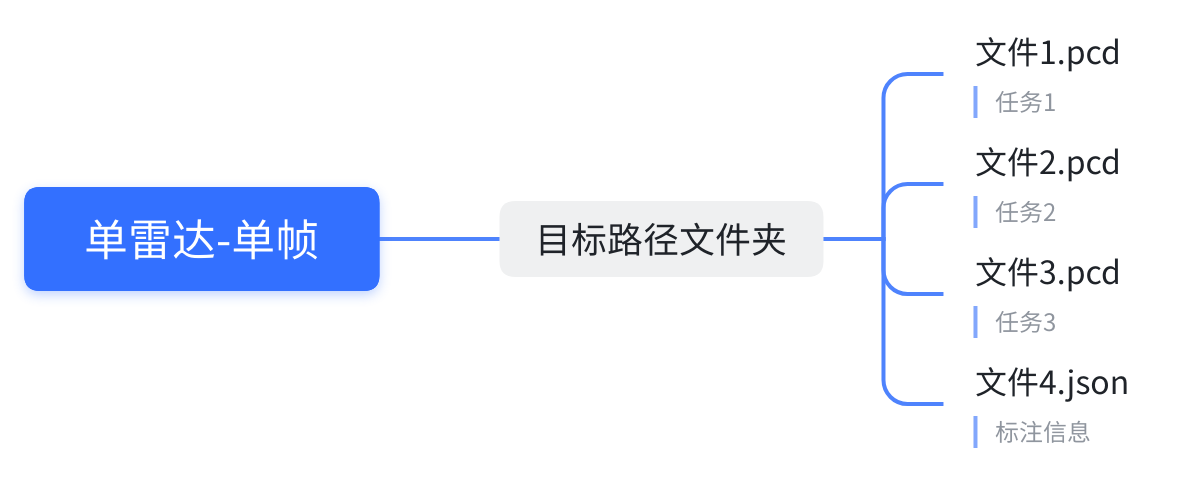
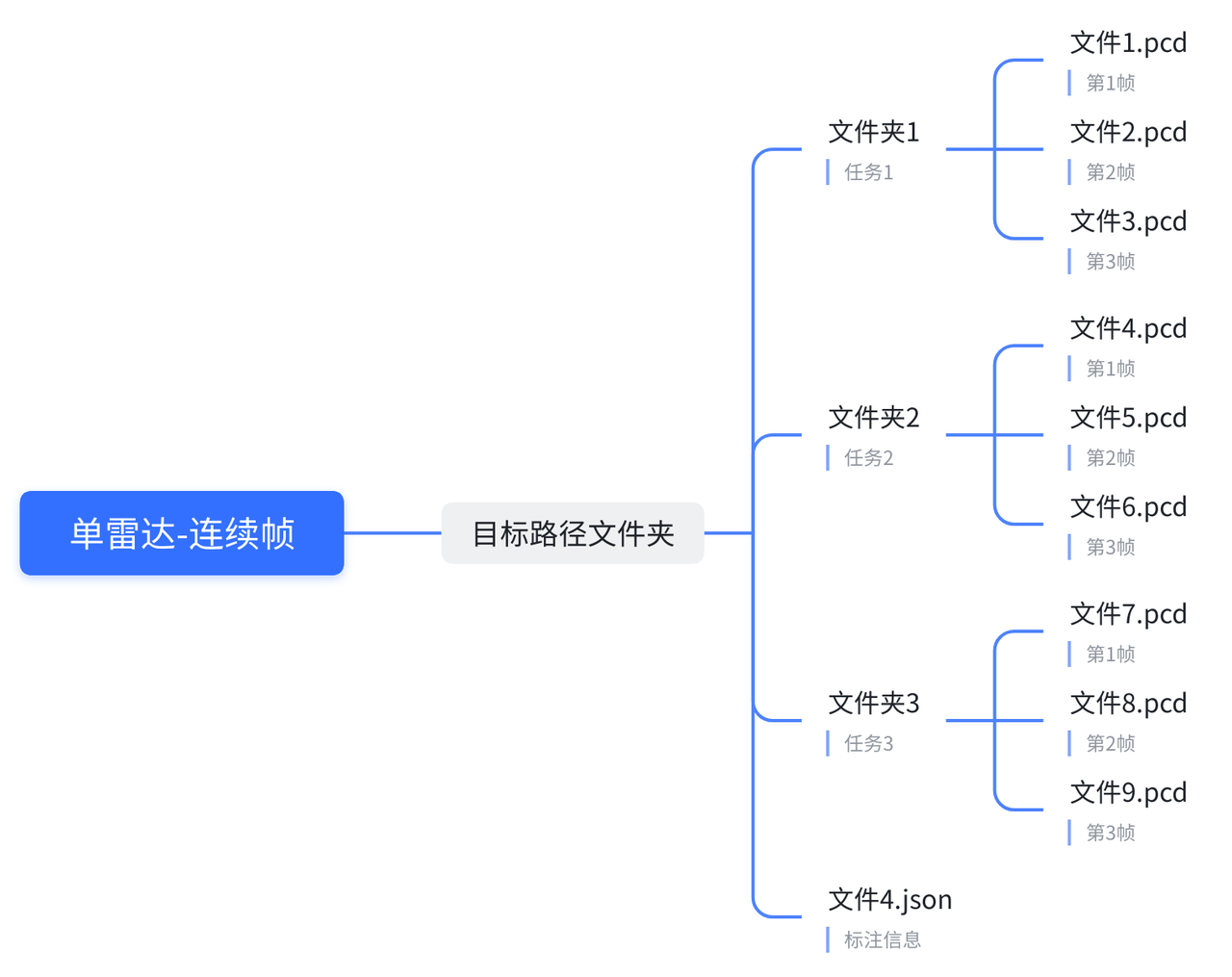
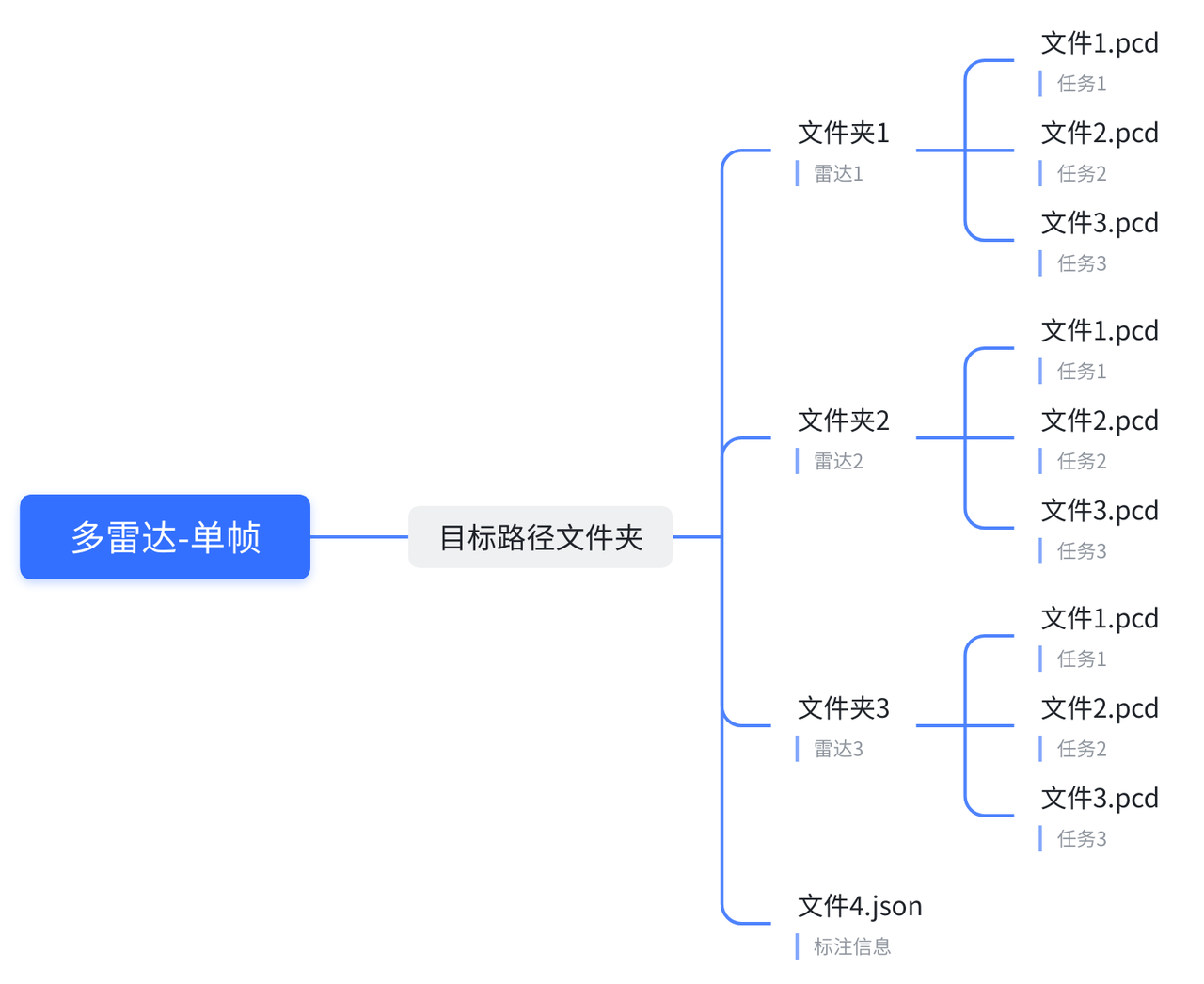
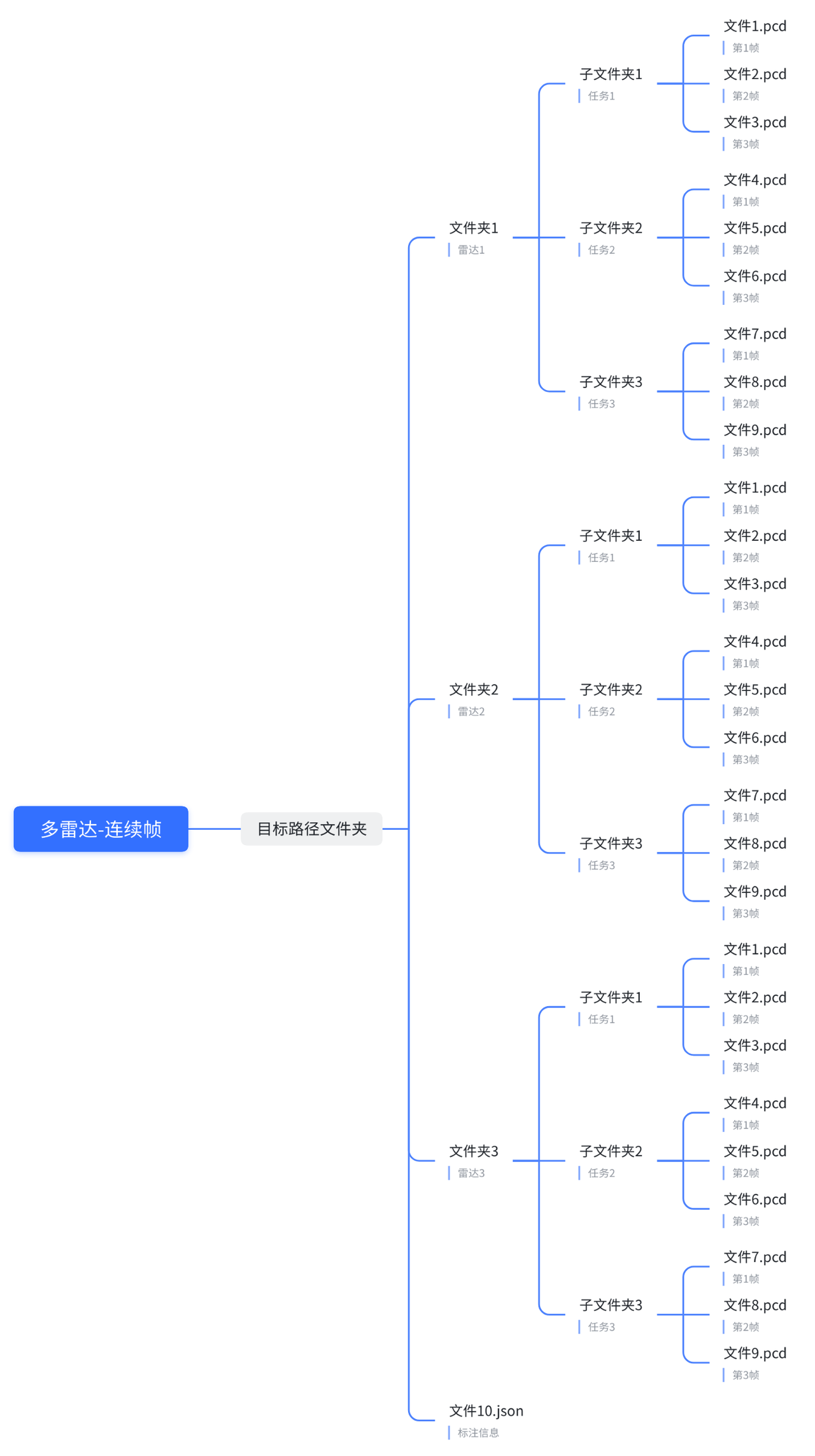
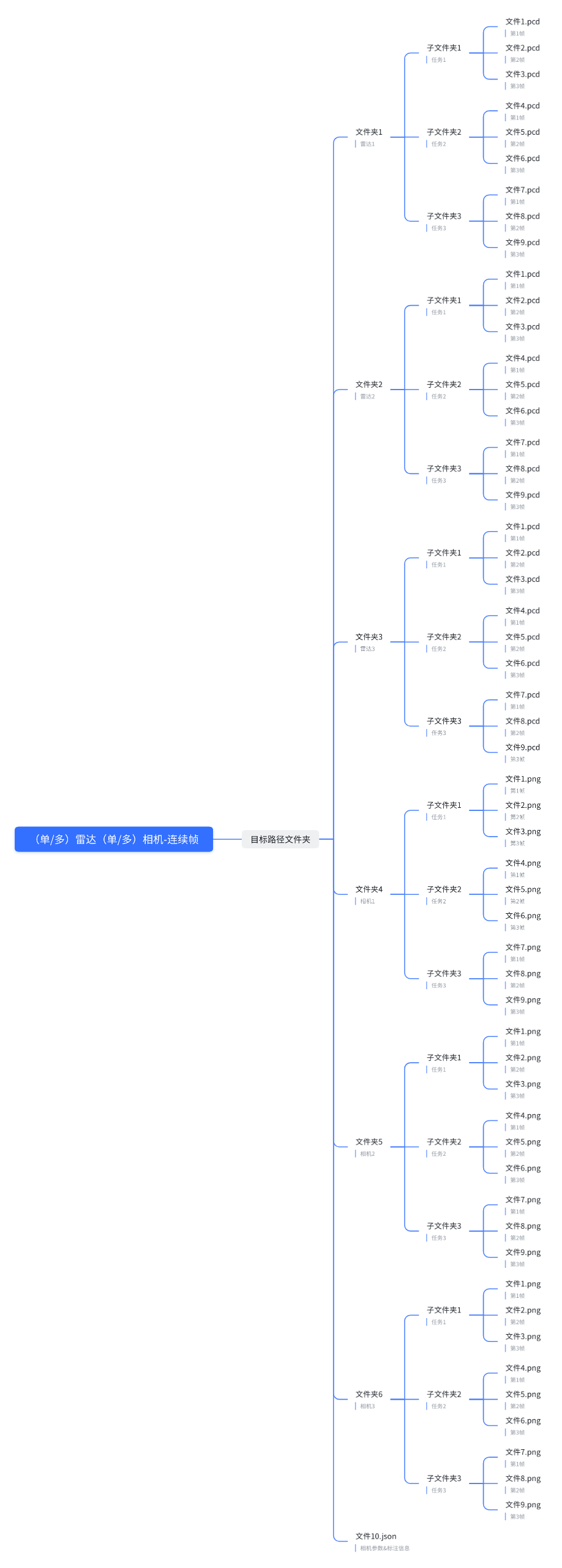
适用于单帧以及连续帧, .json 文件为每个相机的独立参数，可配置内容参照 相机参数 部分

  -data_root
    -Camera1
        1620724790.jpg
        1620724791.jpg
        ...
     Camera1.json

    -Camera2
        1620724790.jpg
        1620724791.jpg
        ...
     Camera2.json

    -Camera3
        1620724790.jpg
        1620724791.jpg
        ...
     Camera3.json

    -Lidar
        1620724790.pcd
        1620724791.pcd
        ...

相机参数

坐标系说明：采用激光雷达坐标系，以自车正前向为x轴正方向的右手系，如果参数坐标系与其不对应则需要进行坐标变换之后给到

外参采用激光雷达坐标系下，相机相对于激光雷达的转换矩阵或者具体参数，如果是雷达相对于相机坐标系的外参矩阵，则需要经过求逆变换处理再给到，以加速数据适配流程

为对应相机文件夹命名的json文件, 内容为 拆解后的具体参数

fov
number
required
object (CameraHeading)

相机朝向，相对点云文件中的原点 (0, 0, 0) 的朝向，四元数

required
object (CameraIntrinsicParameter)

相机内参

matrix
Array of numbers[ items ]

Bev 映射矩阵

maxz
number
minz
number
required
object (PointCloudCoordinate)

相机位置，相对点云文件中的原点 (0, 0, 0) 的位置

projection
Array of numbers[ items ]
required
object (CameraRadial)

相机径向畸变参数

skew
required
number

相机扭曲因子

required
object (CameraTangential)

相机切向畸变参数

type
required
string (CameraType)
Enum: "PinHole" "Fisheye" "OmniDirectional" "Bev"

相机类型

unProjection
Array of numbers[ items ]
{
  • "type": "PinHole",
  • "heading": {
    },
  • "position": {
    },
  • "intrinsic": {
    },
  • "skew": 0,
  • "radial": {
    },
  • "tangential": {
    },
  • "imageWidth": 1080,
  • "imageHeight": 960
}

点云

required
object (PointCloudSource)

单帧点云数据源

attachmentType
required
string

单帧点云输入类型为POINTCLOUD

Value: "POINTCLOUD"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (PointCloudDataRecordMetadata)

点云标注可能用到的 metadata 信息

{
  • "attachmentType": "POINTCLOUD",
  • "metadata": {
    },
  • "attachment": {
    }
}

点云序列

required
Array of objects (PointCloudSource) [ items ]

点云序列数据源

attachmentType
required
string

点云序列输入类型为POINTCLOUD_SEQUENCE

Value: "POINTCLOUD_SEQUENCE"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (PointCloudDataRecordMetadata)

点云标注可能用到的 metadata 信息

{
  • "attachmentType": "POINTCLOUD_SEQUENCE",
  • "metadata": {
    },
  • "attachment": [
    ]
}

图像类

图片

required
string or ImageSourceEntity (object) or Array of ImageSourceEntity (objects) (ImageSource)

单帧图片输入数据链接

attachmentType
required
string

单帧图片输入类型为IMAGE

Value: "IMAGE"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (ImageDataRecordMetadata)

图片标注可能用到的 metadata 信息

{}

图片序列

required
Array of strings or ImageSourceEntity (object) or Array of ImageSourceEntity (objects) (ImageSource) [ items ]

图片序列输入数据链接，为一个有序的Array

attachmentType
required
string

图片序列输入类型为IMAGE_SEQUENCE

Value: "IMAGE_SEQUENCE"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (ImageDataRecordMetadata)

图片标注可能用到的 metadata 信息

{}

视频

attachment
required
string

视频数据链接

attachmentType
required
string

视频数据类型为VIDEO

Value: "VIDEO"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (VideoDataRecordMetadata)

视频标注可能用到的 metadata 信息

{
  • "attachmentType": "VIDEO",
  • "attachment": "https://torb.now.sh/road.mp4",
  • "metadata": {
    }
}

文本类

文本

attachment
required
string

文本数据链接

attachmentType
required
string

文本数据类型为TEXT

Value: "TEXT"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (TextDataRecordMetadata)

文本标注可能用到的 metadata 信息

{}

音频类

音频

attachment
required
string

音频数据链接

attachmentType
required
string

音频数据类型为AUDIO

Value: "AUDIO"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (AudioDataRecordMetadata)

音频标注可能用到的 metadata 信息

{}

数据集创建的数据存放路径

文本

图像

单相机-单帧

单相机-连续帧

多相机-单帧

多相机-连续帧

点云

单雷达-单帧

单雷达-连续帧

多雷达-单帧

多雷达-连续帧

（单/多）雷达（单/多）相机-单帧

（单/多）雷达（单/多）相机-连续帧

音频

视频

命名要求

  1. 点云映射标注场景需要区分出雷达和相机文件夹
  • 雷达：lidar-雷达名称
  • 主雷达：mainlidar-雷达名称
  • 相机：camera-相机名称

预标注样例

单一矩形框任务

required
string or ImageSourceEntity (object) or Array of ImageSourceEntity (objects) (ImageSource)

单帧图片输入数据链接

attachmentType
required
string

单帧图片输入类型为IMAGE

Value: "IMAGE"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (ImageDataRecordMetadata)

图片标注可能用到的 metadata 信息

{
  • "attachmentType": "IMAGE",
  • "attachment": "https://yourwebsite.com/projects/investor_video_tempfile/fruit.jpg",
  • "metadata": {
    }
}

单一多边形框任务

required
string or ImageSourceEntity (object) or Array of ImageSourceEntity (objects) (ImageSource)

单帧图片输入数据链接

attachmentType
required
string

单帧图片输入类型为IMAGE

Value: "IMAGE"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (ImageDataRecordMetadata)

图片标注可能用到的 metadata 信息

{
  • "attachmentType": "IMAGE",
  • "attachment": "https://yourwebsite.com/projects/investor_video_tempfile/fruit.jpg",
  • "metadata": {
    }
}

多边形加2个输入项父子结构

required
string or ImageSourceEntity (object) or Array of ImageSourceEntity (objects) (ImageSource)

单帧图片输入数据链接

attachmentType
required
string

单帧图片输入类型为IMAGE

Value: "IMAGE"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (ImageDataRecordMetadata)

图片标注可能用到的 metadata 信息

{
  • "attachmentType": "IMAGE",
  • "attachment": "https://yourwebsite.com/projects/investor_video_tempfile/fruit.jpg",
  • "metadata": {
    }
}

文本选择加输入项父子结构

attachment
required
string

文本数据链接

attachmentType
required
string

文本数据类型为TEXT

Value: "TEXT"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (TextDataRecordMetadata)

文本标注可能用到的 metadata 信息

{
  • "attachmentType": "TEXT",
  • "attachment": "https://yourwebsite.com/b7853399-5d21-46ae-82e4-b58ea4c29aac.txt",
  • "metadata": {
    }
}

单一3D框

required
Array of objects (PointCloudSource) [ items ]

点云序列数据源

attachmentType
required
string

点云序列输入类型为POINTCLOUD_SEQUENCE

Value: "POINTCLOUD_SEQUENCE"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (PointCloudDataRecordMetadata)

点云标注可能用到的 metadata 信息

{
  • "attachmentType": "POINTCLOUD_SEQUENCE",
  • "attachment": [],
  • "metadata": {
    }
}

3D框+2D框映射

required
Array of objects (PointCloudSource) [ items ]

点云序列数据源

attachmentType
required
string

点云序列输入类型为POINTCLOUD_SEQUENCE

Value: "POINTCLOUD_SEQUENCE"
extraInfoUrls
Array of strings

额外参考信息，可以为 url 链接或文字，需要是一个Array

object (PointCloudDataRecordMetadata)

点云标注可能用到的 metadata 信息

{
  • "attachmentType": "POINTCLOUD_SEQUENCE",
  • "attachment": {},
  • "metadata": {
    }
}

导入样例

通用部分

required
Array of AnnotationSlot (object) or AnnotationSlotChildren (object) or AnnotationInput (object) or AnnotationAnchor (object) or AnnotationChildrenOnly (object) (Annotation) [ items ]

当前任务所有标注结果

Array of AnnotationSlot (object) or AnnotationSlotChildren (object) or AnnotationInput (object) or AnnotationAnchor (object) or AnnotationChildrenOnly (object) (Annotation) [ items ]
required
Array of AnnotationMisplacedIssue (object) or AnnotationExtraIssue (object) or AnnotationMissingIssue (object) (AnnotationIssue) [ items ]
object

当前任务辅助标注结果的metadata信息

required
Array of objects (AnnotationNote) [ items ]
{
  • "annotations": [
    ],
  • "hints": [
    ],
  • "issues": [
    ],
  • "metadata": {
    },
  • "notes": [
    ]
}

导出结果

通用部分

required
Array of AnnotationSlot (object) or AnnotationSlotChildren (object) or AnnotationInput (object) or AnnotationAnchor (object) or AnnotationChildrenOnly (object) (Annotation) [ items ]

当前任务所有标注结果

Array of AnnotationSlot (object) or AnnotationSlotChildren (object) or AnnotationInput (object) or AnnotationAnchor (object) or AnnotationChildrenOnly (object) (Annotation) [ items ]
required
Array of AnnotationMisplacedIssue (object) or AnnotationExtraIssue (object) or AnnotationMissingIssue (object) (AnnotationIssue) [ items ]
object

当前任务辅助标注结果的metadata信息

required
Array of objects (AnnotationNote) [ items ]
{
  • "annotations": [
    ],
  • "hints": [
    ],
  • "issues": [
    ],
  • "metadata": {
    },
  • "notes": [
    ]
}

操作项样例

矩形框

key
required
string

操作项的id，用来区分同类型的不同操作项。比如两个Box2d操作项一个标记苹果，另一个标记鸭梨

label
required
string

操作项的名字

required
Array of TextSlot (object) or Box2dSlot (object) or Box3DSlot (object) or SemanticSegmentation2DSlot (object) or SemanticSegmentation3DSlot (object) or PointSlot (object) or Point3DSlot (object) or LineSlot (object) or Line3DSlot (object) or SplinesSlot (object) or CuboidSlot (object) or PolygonSlot (object) or Polygon3DSlot (object) or AudioRecordingSlot (object) or TimeSliceSlot (object) or FileSlot (object) (Slot) [ items ]

操作项产生的一系列标记结果。同一个任务中可出现多个目标需要用当前操作项标记，例如多个苹果

type
required
string

操作项的类型为slot

Value: "slot"
{
  • "key": "box2d-[ae65e]",
  • "label": "橘子",
  • "type": "slot",
  • "slots": [
    ]
}

文本选择

key
required
string

操作项的id，用来区分同类型的不同操作项。比如两个Box2d操作项一个标记苹果，另一个标记鸭梨

label
required
string

操作项的名字

required
Array of TextSlot (object) or Box2dSlot (object) or Box3DSlot (object) or SemanticSegmentation2DSlot (object) or SemanticSegmentation3DSlot (object) or PointSlot (object) or Point3DSlot (object) or LineSlot (object) or Line3DSlot (object) or SplinesSlot (object) or CuboidSlot (object) or PolygonSlot (object) or Polygon3DSlot (object) or AudioRecordingSlot (object) or TimeSliceSlot (object) or FileSlot (object) (Slot) [ items ]

操作项产生的一系列标记结果。同一个任务中可出现多个目标需要用当前操作项标记，例如多个苹果

type
required
string

操作项的类型为slot

Value: "slot"
{
  • "key": "text-[21d18]",
  • "type": "slot",
  • "label": "公司",
  • "slots": [
    ]
}

2D长方体

key
required
string

操作项的id，用来区分同类型的不同操作项。比如两个Box2d操作项一个标记苹果，另一个标记鸭梨

label
required
string

操作项的名字

required
Array of TextSlot (object) or Box2dSlot (object) or Box3DSlot (object) or SemanticSegmentation2DSlot (object) or SemanticSegmentation3DSlot (object) or PointSlot (object) or Point3DSlot (object) or LineSlot (object) or Line3DSlot (object) or SplinesSlot (object) or CuboidSlot (object) or PolygonSlot (object) or Polygon3DSlot (object) or AudioRecordingSlot (object) or TimeSliceSlot (object) or FileSlot (object) (Slot) [ items ]

操作项产生的一系列标记结果。同一个任务中可出现多个目标需要用当前操作项标记，例如多个苹果

type
required
string

操作项的类型为slot

Value: "slot"
{
  • "key": "cuboid-[066e9]",
  • "label": "汽车",
  • "type": "slot",
  • "slots": [
    ]
}

操作项类型

文本选择

confidence
number

当前预标文本标记匹配度

confirmed
boolean

当前预标文本标记是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
id
required
string

当前文本标记实例的id

label
required
string

当前文本标记实例的名称

length
number

当前文本标记实例的选中文本长度

object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

selection
string
source
string
start
number

当前文本标记实例的选中文本的起始位置

teamId
number

辅助大数据统计的字段

text
required
string

当前文本标记实例的选中文本内容

type
required
string

文本标记实例的类型为text

Value: "text"
userId
number

辅助大数据统计的字段

{
  • "id": "ab662508-c2da-4b71-9e1b-ef4b451aaf3a",
  • "label": "图片说明",
  • "length": 20,
  • "start": 71,
  • "text": "在海口热带农业科技博览园拍摄的沙漠玫瑰。",
  • "type": "text"
}

2D矩形框

binding
boolean
confidence
number

当前预标Box2d标记匹配度

confirmed
boolean

当前预标Box2d标记是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
id
required
string

当前Box2d标记实例的id

label
required
string

当前Box2d标记实例的名称

object (AnnotationBaseMetadata)
required
object (Plane)

当前Box2d标记实例的平面位置信息

poolId
number

辅助大数据统计的字段

source
string
teamId
number

辅助大数据统计的字段

object (TimeSeries%3CPlane%3E)
type
required
string

Box2d标记实例的类型为box2d

Value: "box2d"
unbindings
Array of strings
userId
number

辅助大数据统计的字段

{
  • "id": "f6933a2f-1d81-406f-a3c9-5f815608cded",
  • "type": "box2d",
  • "label": "2D框",
  • "plane": {
    }
}

3D框

坐标系说明：采用激光雷达坐标系，以自车正前向为x轴正方向的右手系

box
required
Array of numbers (Box3D) [ items ]

当前Box3D标记实例的位置信息，默认为一个matrix4，从中可以获取到偏转角、位置以及大小信息。

confidence
number

当前预标Box3D标记匹配度

confirmed
boolean

当前预标Box3D标记是否应用到实际标注

consistent
boolean
coordinate
string (InterpolatedCoordinate)
Enum: "world" "local"
hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
id
required
string

当前Box3D标记实例的id

immovable
boolean
label
required
string

当前Box3D标记实例的名称

object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

source
string
teamId
number

辅助大数据统计的字段

object (TimeSeries%3CBox3D%3E)
type
required
string

Box3D标记实例的类型为box3d

Value: "box3d"
unbindings
Array of strings
userId
number

辅助大数据统计的字段

{
  • "id": "fd969829-840c-41bd-8fd4-a257d155b30a",
  • "box": [
    ],
  • "type": "box3d",
  • "label": "3D框"
}

点

binding
boolean
confidence
number

当前预标点标记匹配度

confirmed
boolean

当前预标点标记是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
id
required
string

当前点标记实例的id

label
required
string

当前点标记实例的名称

object (AnnotationBaseMetadata)
required
object (Point)

当前点标记实例的点位置信息

poolId
number

辅助大数据统计的字段

source
string
teamId
number

辅助大数据统计的字段

object (TimeSeries%3CPoint%3E)
type
required
string

直线标记实例的类型为point

Value: "point"
unbindings
Array of strings
userId
number

辅助大数据统计的字段

{
  • "id": "3f24479a-88b0-42f1-ba6b-e4d1eacf55ef",
  • "type": "point",
  • "label": "关键点",
  • "point": {
    }
}

直线

binding
boolean
confidence
number

当前预标直线标记匹配度

confirmed
boolean

当前预标直线标记是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
id
required
string

当前直线标记实例的id

label
required
string

当前直线标记实例的名称

object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

source
string
teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cdef-alias-986760303-189-252-986760303-0-5593%5B%5D%3E)
type
required
string

直线标记实例的类型为line

Value: "line"
unbindings
Array of strings
userId
number

辅助大数据统计的字段

required
Array of objects (Point) [ items ]

当前直线标记实例的点位置信息

{
  • "id": "29d45554-d7aa-413a-bbe1-5684c5a2ed78",
  • "type": "line",
  • "label": "车道线",
  • "vertices": [
    ]
}

曲线

binding
boolean
confidence
number

当前预标曲线标记匹配度

confirmed
boolean

当前预标曲线标记是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
id
required
string

当前曲线标记实例的id

label
required
string

当前曲线标记实例的名称

object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

source
string
teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cdef-alias-986760303-189-252-986760303-0-5593%5B%5D%3E)
type
required
string

曲线标记实例的类型为splines

Value: "splines"
unbindings
Array of strings
userId
number

辅助大数据统计的字段

required
Array of objects (Point) [ items ]

当前曲线标记实例的点位置信息

{
  • "id": "408ef583-c76f-4e4a-9392-7711bd15f901",
  • "type": "splines",
  • "label": "分割线",
  • "vertices": [
    ]
}

长方体

binding
boolean
confidence
number

当前预标Cuboid标记匹配度

confirmed
boolean

当前预标Cuboid标记是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
id
required
string

当前Cuboid标记实例的id

label
required
string

当前Cuboid标记实例的名称

object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

source
string
teamId
number

辅助大数据统计的字段

object (TimeSeries%3CCuboidVertices%3E)
type
required
string

Cuboid标记实例的类型为cuboid

Value: "cuboid"
unbindings
Array of strings
userId
number

辅助大数据统计的字段

required
object (CuboidVertices)

当前Cuboid标记实例的位置信息

{
  • "id": "21255fbb-58ab-4a28-bd7f-db8e208b363e",
  • "type": "cuboid",
  • "label": "立体框",
  • "vertices": {
    }
}

多边形

binding
boolean
object (BoundaryIndex)
confidence
number

当前预标多边形标记匹配度

confirmed
boolean

当前预标多边形标记是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
id
required
string

当前多边形标记实例的id

Array of objects (InteractiveSegmentationPoint) [ items ]
label
required
string

当前多边形标记实例的名称

object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

source
string
teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cdef-alias-986760303-189-252-986760303-0-5593%5B%5D%3E)
type
required
string

多边形标记实例的类型为polygon

Value: "polygon"
unbindings
Array of strings
userId
number

辅助大数据统计的字段

required
Array of objects (Point) [ items ]

当前多边形标记实例的点位置信息

{
  • "id": "f6ec27a8-c722-42b8-8968-2b32b30ebee6",
  • "type": "polygon",
  • "label": "多边形框",
  • "vertices": [
    ]
}

3D语义分割

confidence
number

当前预标3D语义分割标记匹配度

confirmed
boolean

当前预标3D语义分割标记是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
id
required
string
label
required
string
object (AnnotationBaseMetadata)
required
number or object or Array of numbers (Selected3DPoints)
poolId
number

辅助大数据统计的字段

source
string
teamId
number

辅助大数据统计的字段

object (TimeSeries%3CSelected3DPoints%3E)
type
required
string
Value: "semantic-segmentation3d"
userId
number

辅助大数据统计的字段

{
  • "id": "ae71bd1a-7756-4203-b08d-e40614f58f1e",
  • "label": "灯杆",
  • "points": [
    ],
  • "timeSeries": {
    },
  • "type": "semantic-segmentation3d"
}

3D多边形

confidence
number

当前预标3D多边形标记匹配度

confirmed
boolean

当前预标3D多边形标记是否应用到实际标注

coordinate
string (InterpolatedCoordinate)
Enum: "world" "local"
hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
id
required
string
immovable
boolean
label
required
string
object (AnnotationBaseMetadata)
required
Array of objects (Point3D) [ items ]
poolId
number

辅助大数据统计的字段

source
string
teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cdef-alias-986760303-252-311-986760303-0-5593%5B%5D%3E)
type
required
string
Value: "polygon3d"
unbindings
Array of strings
userId
number

辅助大数据统计的字段

{
  • "id": "d0009254-a3ca-40ce-a5ec-0f1a6540ca95",
  • "label": "车道线",
  • "points": [
    ],
  • "type": "polygon3d"
}

3D直线

confidence
number
confirmed
boolean
coordinate
string (InterpolatedCoordinate)
Enum: "world" "local"
hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
id
required
string
immovable
boolean
label
required
string
object (AnnotationBaseMetadata)
required
Array of objects (Point3D) [ items ]
poolId
number

辅助大数据统计的字段

source
string
teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cdef-alias-986760303-252-311-986760303-0-5593%5B%5D%3E)
type
required
string
Value: "line3d"
unbindings
Array of strings
userId
number

辅助大数据统计的字段

{
  • "id": "bd57c6a9-e9e4-42f9-b85d-8b95e05048aa",
  • "label": "车道线",
  • "points": [
    ],
  • "type": "line3d"
}

3D点

confidence
number
confirmed
boolean
coordinate
string (InterpolatedCoordinate)
Enum: "world" "local"
hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
id
required
string
immovable
boolean
label
required
string
object (AnnotationBaseMetadata)
required
object (Point3D)
poolId
number

辅助大数据统计的字段

source
string
teamId
number

辅助大数据统计的字段

object (TimeSeries%3CPoint3D%3E)
type
required
string
Value: "point3d"
unbindings
Array of strings
userId
number

辅助大数据统计的字段

{
  • "id": "76e90359-ca87-4098-a880-ebcbdfeda444",
  • "label": "3D关键点",
  • "point": {
    },
  • "type": "point3d"
}

输入项样例

单选题

consistentAttribute
boolean
required
InputBoolean (object) or InputNumber (object) or InputText (object) or InputSelect (object) or InputNestedSelect (object) or InputMultipleSelect (object) or InputMultipleText (object) or InputMultipleNestedSelect (object) or InputPosture3D (object) (InputValue)

输入项的结果数据结构，输入项包括：数字、文本、单选、多选、嵌套单选、嵌套多选等

key
required
string

输入项的id，用来区分同类型的不同输入项。比如两个单选题输入项一个标记颜色，另一个标记形状

label
required
string

输入项的名字

type
required
string

输入项的类型为input

Value: "input"
{
  • "key": "input-select-语种",
  • "label": "语种",
  • "type": "input",
  • "input": {
    }
}

文本输入

consistentAttribute
boolean
required
InputBoolean (object) or InputNumber (object) or InputText (object) or InputSelect (object) or InputNestedSelect (object) or InputMultipleSelect (object) or InputMultipleText (object) or InputMultipleNestedSelect (object) or InputPosture3D (object) (InputValue)

输入项的结果数据结构，输入项包括：数字、文本、单选、多选、嵌套单选、嵌套多选等

key
required
string

输入项的id，用来区分同类型的不同输入项。比如两个单选题输入项一个标记颜色，另一个标记形状

label
required
string

输入项的名字

type
required
string

输入项的类型为input

Value: "input"
{
  • "key": "input-text-email",
  • "label": "Email",
  • "type": "input",
  • "input": {
    }
}

嵌套多选

consistentAttribute
boolean
required
InputBoolean (object) or InputNumber (object) or InputText (object) or InputSelect (object) or InputNestedSelect (object) or InputMultipleSelect (object) or InputMultipleText (object) or InputMultipleNestedSelect (object) or InputPosture3D (object) (InputValue)

输入项的结果数据结构，输入项包括：数字、文本、单选、多选、嵌套单选、嵌套多选等

key
required
string

输入项的id，用来区分同类型的不同输入项。比如两个单选题输入项一个标记颜色，另一个标记形状

label
required
string

输入项的名字

type
required
string

输入项的类型为input

Value: "input"
{
  • "key": "multiple-nested-select-[193ca]",
  • "label": "物体类型",
  • "type": "input",
  • "input": {
    }
}

输入项类型

布尔值

confidence
number

当前预标输入项-布尔值匹配度

confirmed
boolean

当前预标输入项-布尔值是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cboolean%3E)
type
required
string

输入项-布尔值的类型为boolean

Value: "boolean"
userId
number

辅助大数据统计的字段

value
boolean or null

输入项-布尔值的保存数据类型为布尔值，即true/false

{
  • "type": "boolean",
  • "value": true
}

数字

confidence
number

当前预标输入项-数值匹配度

confirmed
boolean

当前预标输入项-数值是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cnumber%3E)
type
required
string

输入项-数值的类型为number

Value: "number"
userId
number

辅助大数据统计的字段

value
number or null

输入项-数值的保存数据类型为数字

{
  • "type": "number",
  • "value": "1"
}

文本

confidence
number

当前预标输入项-文本匹配度

confirmed
boolean

当前预标输入项-文本是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cstring%3E)
type
required
string

输入项-文本的类型为text

Value: "text"
userId
number

辅助大数据统计的字段

value
string or null

输入项-文本的保存数据类型为string，即字符串

{
  • "type": "text",
  • "value": "abc@abc.com"
}

单选

confidence
number

当前预标输入项-嵌套单选匹配度

confirmed
boolean

当前预标输入项-嵌套单选是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cstring%3E)
type
required
string

输入项-嵌套单选的类型为select

Value: "select"
userId
number

辅助大数据统计的字段

value
string or null

输入项-单选的保存数据类型为string，即字符串

{
  • "type": "select",
  • "value": "英文"
}

嵌套单选

confidence
number

当前预标输入项-嵌套匹配度

confirmed
boolean

当前预标输入项-嵌套是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cstring%5B%5D%3E)
type
required
string

输入项-嵌套单选的类型为nested-select

Value: "nested-select"
userId
number

辅助大数据统计的字段

Array of strings or null

输入项-嵌套单选的保存数据类型为string array，即字符串的一个数组

{
  • "type": "nested-select",
  • "value": [
    ]
}

多选

confidence
number

当前预标输入项-多选匹配度

confirmed
boolean

当前预标输入项-多选是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cstring%5B%5D%3E)
type
required
string

输入项-多选的类型为multiple-select

Value: "multiple-select"
userId
number

辅助大数据统计的字段

Array of strings or null

输入项-多选的保存数据类型为string array，即字符串的一个数组

{
  • "type": "multiple-select",
  • "value": [
    ]
}

标签

confidence
number

当前预标输入项-标签模式匹配度

confirmed
boolean

当前预标输入项-标签模式是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cstring%5B%5D%3E)
type
required
string

输入项-标签模式的类型为multiple-text

Value: "multiple-text"
userId
number

辅助大数据统计的字段

Array of strings or null

输入项-标签模式的保存数据类型为string array，即字符串的一个数组

{
  • "type": "multiple-text",
  • "value": [
    ]
}

嵌套多选

confidence
number

当前预标输入项-嵌套多选匹配度

confirmed
boolean

当前预标输入项-嵌套多选是否应用到实际标注

hintConfidence
string (HintConfidence)
Enum: "High" "Medium" "Low"
hintStatus
string (HintStatus)
Enum: "Unconfirmed" "Accepted" "Modified" "Rejected" "Draft" "Frozen" "Compared"
object (AnnotationBaseMetadata)
poolId
number

辅助大数据统计的字段

teamId
number

辅助大数据统计的字段

object (TimeSeries%3Cstring%5B%5D%3E)
type
required
string

输入项-嵌套多选的类型为multiple-nested-select

Value: "multiple-nested-select"
userId
number

辅助大数据统计的字段

Array of strings or null

输入项-嵌套多选的保存数据类型为string array，即字符串的一个数组

{
  • "type": "multiple-nested-select",
  • "value": [
    ]
}

父子结构的操作项样例

多边形加单选题

key
required
string

父子结构的操作项的id，用来区分同类型的不同父子结构的操作项。比如两个Box2d + inputSelect的父子结构操作项，一个标记汽车以及汽车的额外属性，另一个标记障碍物以及障碍物的额外属性

label
required
string

父子结构的操作项的名字

required
Array of objects (SlotChildren) [ items ]

父子结构的操作项产生的一系列标记结果。同一个任务中可出现多个目标需要用当前父子结构的操作项标记，例如多个汽车

type
required
string

父子结构的操作项的类型为slotChildren

Value: "slotChildren"
{
  • "key": "polygon-[82bb6]",
  • "label": "形状",
  • "type": "slotChildren",
  • "slotsChildren": [
    ]
}

3D框加多个矩形框

key
required
string

父子结构的操作项的id，用来区分同类型的不同父子结构的操作项。比如两个Box2d + inputSelect的父子结构操作项，一个标记汽车以及汽车的额外属性，另一个标记障碍物以及障碍物的额外属性

label
required
string

父子结构的操作项的名字

required
Array of objects (SlotChildren) [ items ]

父子结构的操作项产生的一系列标记结果。同一个任务中可出现多个目标需要用当前父子结构的操作项标记，例如多个汽车

type
required
string

父子结构的操作项的类型为slotChildren

Value: "slotChildren"
{
  • "key": "car",
  • "label": "小汽车",
  • "type": "slotChildren",
  • "slotsChildren": [
    ]
}

多边形加多个输入项

key
required
string

父子结构的操作项的id，用来区分同类型的不同父子结构的操作项。比如两个Box2d + inputSelect的父子结构操作项，一个标记汽车以及汽车的额外属性，另一个标记障碍物以及障碍物的额外属性

label
required
string

父子结构的操作项的名字

required
Array of objects (SlotChildren) [ items ]

父子结构的操作项产生的一系列标记结果。同一个任务中可出现多个目标需要用当前父子结构的操作项标记，例如多个汽车

type
required
string

父子结构的操作项的类型为slotChildren

Value: "slotChildren"
{
  • "key": "polygon-[0c83e]",
  • "type": "slotChildren",
  • "label": "多边形框+转写",
  • "slotsChildren": [
    ]
}

通用交换数据

独立标注工具支持的输入方式:

1. URL Hash 传值

2. json文件地址

文本标注实例

示例地址

Array of objects (ProjectAlgorithm) [ items ]

算法辅助

callbackURL
string

标注结果提交地址

required
object or object
object (TaskResult)

当前任务导出结果

{
  • "taskParams": {
    },
  • "taskResult": {
    }
}